Rumus Volume Tabung – Dalam mata pelajaran matematika ada beberapa bangun ruang yang mana salah satunya adalah Tabung. Tabung adalah salah satu bangun ruang yang dibatasi dengan dua sisi yang kongruen dan sejajar dengan bentuk melingkar atau lingkaran. Namun masih banyak orang yang belum mengetahui apa itu tabung, kali ini essay.co.id akan menjeaskan tentang apa itu tabung dan rumus volume tabung.
Pengertian Bangun Ruang (Tabung)
Tabung merupakan salah satu bangun ruang yang mana di batasi oleh dua sisi yang bentuk lingkarang dan pada bagian alasnya memiliki bidang yang melengkung yang disebut juga dengan selimut tabung.
Sifat – Sifat Tabung
- Terdapat 2 sisi berbentuk lingkaran dan sisi yang satunya lagi memiliki bidang lengkung atau disebut juga dengan selimut tabung
- Memiliki 2 rusuk lengkung
- Tidak memiliki titik sudut
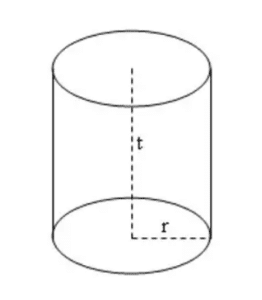
Gambar tabung
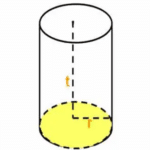
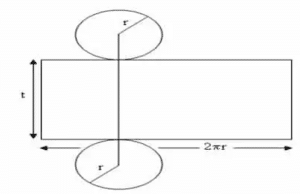
Jika tabung yang ada diatas itu dibuka dan bagian sisi alasnya dipotong maka dapat seperti jaring jaring dibawah ini.
- pada bidan alas dan bidang atas memiliki bentuk lingkaran dengan jari-jari yang sama.
- Tinggi tabung merupakan jarak antara titik antara pusat lingkaran alas dan atas.
Unsur – Unsur Tabung
- Memiliki 3 sisi yaitu sisi atas, bawah dan sisi lengkung (disebut juga dengan selimut tabung), sisi atas dan bawah memiliki bentuk lingkarang yang bentuk dan ukurunnnya sama.
- Memiliki 2 rusuk yang masing-masing rusuk tersebut memiliki bentuk lingkaran
- Tabung tidak memiliki titik sudut.

- Jarak antar bidang atas dan bawah disebut dengan tinggi dari tabung
Luas Permukaan Tabung
Untuk luas permukaan tabung sendiri bisa kita lihat dari jaring-jaring tabung, yang mana jaring jaring tersebut dari persegi panjang dan dua daerah lingkarang yang sama besar. Pada bagian persegi penjang untuk panjangnya sama dengan keliling lingkkaran alas dan atas dari tabung tersebut untuk lebarnya sendiri sama dengan tinggi tabung.
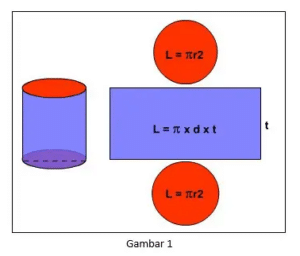
Rumus Luas Tabung
Luas Bidang Lengkung Tabung = Luas Persegi penjang
= p x l
= Keliling lingkaran x tinggi tabung
= (2π) x (t)
= 2π r t
Luas Seluruh Permukaan Tabung = Luas Seluruh Bidang Sisi Tabung
= Luas Bidang Lengkung Tabung + 2 Luas Alas (Lingkaran)
= 2πrt + 2 (πr2)
= 2πr (r + t)

Rumus Tabung
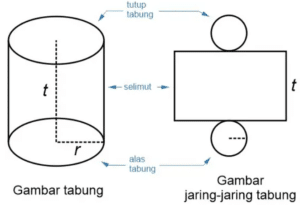
t = tinggi
jari-jari (r) = d÷2
diameter (d) = 2×r
π = 22/7
Rumus volume tabung
V = π × r × r × t
V = π × r² × t
Volume Tabung
Apabila anda disini ingin menentukan volume tabung, maka disini kita lihat sebagai bangun yang terjadi dari prisma beraturan yang memiliki banyak sisi tak terhitung. Maka dari itu keliling dari luas alas sangat dekat dengan keliling dan luas lingkaran. Sedangkan untuk prismanya sendiri itu adalah tinggi dari tabung tersebut,
Bisa dikatakan bahwa volume dari sebuah silinder sama seperti limit volume prismas beraturan yang banyak dari sisinya bertambah sampai tak terhingga.
Jika r itu jari jari bidang alas tabung (berbentuk lingkaran) dan t adalah tinggi dari tabung maka:
Rumus Volume Tabung
Luas Alas x Tinggi
= π × r² × t
Bidang Singgung Pada Bidang Tabung
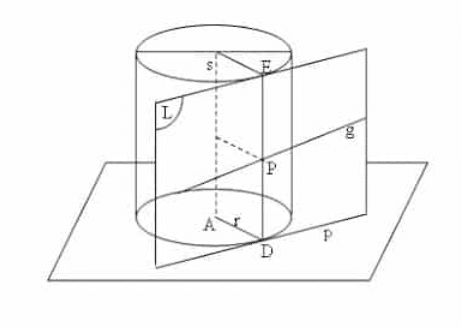
Jika dilihat pada gambar A adalah pusat dari lingkaran alas tabung. Lalu buat garis singgung pada p pada adalas tabung itu di D yang mana sebagai titik singgungnya. Setelah itu dibuatkan garis pelukis DE, maka bidang yang melewati P dan De adalah bidang singgung pada tabung. Namun apabila dalam bidang singgung yang ada di tabung itu kita lukis dengan garis g yang tidak sejajar, maka garis g tersebut akan memotong garis DE di sebuah titik P yang mana merupakan titik persekutuan dari garis g dan bidang tabung.
Dari yang dijelaskan maka dari itu garis g ini disebut menyinggung bidang tabung di titik P. Garis g ini adalah garis yang menyimpang pada sumbu tabung dengan jarak tetap, yaitu r.
Karena bidang singgung L ini melewati garis yang letaknya selalu sejaja dengan sumbu s, maka berakibat setiap bidang singgung pada tabung tersebut letaknya pasti sejajar dengan sumbu tabung s.
Dari pernyataan yang dijabarkan diatas bisa disimpulkan bahwa:
- Semua garis yang menyilang pada garis s dengan jarak tetap (r) yang letaknya sendiri pada bidang yang menyinggung bidang tabung dengan ssebagai sumbu dan r adalah jari-jarinya.
- Setiap bidang yang sejajar dengan garis s dan memiliki jarak tetap (r) terhadap s, menyingging dengan bidang s yang merupakan sebagai sumbu dan r merupakan sebagai jari-jari.
Contoh Soal Rumus Volume Tabung
Ada seorang yang sedang menjual minyak dengan menggunakan sebuah drum yang berntuk seperti tabung untuk menyimpan minyaknya. Jari-jari dari alas drum tersebut adalah 70cm dan tingginya 100cm. Berapa liter minyak yang bisa masuk dalam drum tersebut?
Jawab : V Jawab : V = π r² x tinggi
V = 22/7 x 70² x 100
V = 1.540.000 cm3 = 1. 540 dm3 = 1.540 liter
Bisa kita simpulkan bahwa jumlah minyak yang bisa ditampung oleh drum tersebut adalah 1.540 liter banyaknya.
Mungkin cukup sekian pembahasan yang dapat saya sampaikan kali ini mengenai rumus volume tabung, semoga pembahasan yang saya sampaikan ini bisa bermanfaat buat anda, sekian terima kasih.

